pymaid.sparseness¶
- pymaid.sparseness(x, which='LTS')[source]¶
Calculate sparseness.
Sparseness comes in two flavors:
Lifetime kurtosis (LTK) quantifies the widths of tuning curves (according to Muench & Galizia, 2016):
![S = \Bigg\{ \frac{1}{N} \sum^N_{i=1} \Big[ \frac{r_i - \overline{r}}{\sigma_r} \Big] ^4 \Bigg\} - 3](../../_images/math/77cd5fc929fb62ca7de3f132a83fa713aa06e3eb.png)
where
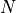 is the number of observations,
is the number of observations, 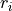 the value of
observation
the value of
observation 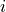 , and
, and 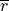 and
and
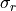 the mean and the standard deviation of the observations’
values, respectively. LTK is assuming a normal, or at least symmetric
distribution.
the mean and the standard deviation of the observations’
values, respectively. LTK is assuming a normal, or at least symmetric
distribution.Lifetime sparseness (LTS) quantifies selectivity (Bhandawat et al., 2007):
![S = \frac{1}{1-1/N} \Bigg[1- \frac{\big(\sum^N_{j=1} r_j / N\big)^2}{\sum^N_{j=1} r_j^2 / N} \Bigg]](../../_images/math/a9ca56cd28a0b5be6f0ba34e2d64eb45e8ba1964.png)
where
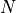 is the number of observations, and
is the number of observations, and 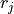 is the
value of an observation.
is the
value of an observation.Notes
NaNvalues will be ignored. You can use that to e.g. ignore zero values in a large connectivity matrix by changing these values toNaNbefore passing it topymaid.sparseness.- Parameters:
x (DataFrame | array-like) – (N, M) dataset with N (rows) observations for M (columns) neurons. One-dimensional data will be converted to two dimensions (N rows, 1 column).
which ("LTS" | "LTK") – Determines whether lifetime sparseness (LTS) or lifetime kurtosis (LTK) is returned.
- Returns:
pandas.Seriesif input was pandas DataFrame, elsenumpy.array.- Return type:
sparseness
Examples
Calculate sparseness of olfactory inputs to group of neurons:
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> # Generate adjacency matrix >>> adj = pymaid.adjacency_matrix(s='annotation:WTPN2017_excitatory_uPN_right', ... t='annotation:ASB LHN') >>> # Calculate lifetime sparseness >>> S = pymaid.sparseness(adj, which='LTS') >>> # Plot distribution >>> ax = S.plot.hist(bins=np.arange(0, 1, .1)) >>> ax.set_xlabel('LTS') >>> plt.show()